ZK的崛起與演變

曾幾何時，零知識證明（以下簡稱ZK）仍然被認為是密碼學教科書中的理論概念，至少在傳統安全研究中很少被主流社群深入探索。然而在Web3.0領域，區塊鏈技術的迅速發展，用短短几年時間實現了ZK從理論到實踐的跨越式進展，一路蓬勃，高歌猛進。

1985年誕生，2014年ZCash才用SNARKs證明了ZK不僅是書本上的傳說，也是實打實的“江湖絕學”，2019年開始，隨着zkSync和Polygon的崛起，ZK從隱私保護的小眾技術，搖身一變成了區塊鏈擴展性問題的關鍵。到了2022年，Tornado Cash轟然倒下，美國財政部的制裁引發了一場關於隱私與自由的廣泛討論，也讓ZK成為了茶餘飯後的熱門話題。2023年起，隨着PLONK、Halo2等新型ZK協議的成熟，ZK技術在區塊鏈領域高速發展，成為Web3.0的新寵。

ZK的崛起不僅僅是因為它在區塊鏈世界中的廣泛應用，也與這些年來不斷創新的開發工具密不可分。儘管這些工具的核心目標都是將代碼邏輯電路化，但幾年間，從最初合約級應用的Circom，到鏈上層為性能優化推出的EVM兼容或等價的zkVM，更新速度之快令人目不暇接，甚至連應用生態腳步都還沒穩住，下一次升級迭代已呼嘯而至。

ZK原理概述

想理解ZK，可以從其共性的漏洞入手。在傳統安全里有個經驗：直接分析代碼邏輯來理清全局往往難度極大，有時不如跑個crash看dump來得直觀，也就是通過漏洞回溯代碼的方式去理解內在邏輯。

初識ZK，可能會被各種專有名詞包圍 — SNARK、STARK、PLONK、QAP、R1CS、Groth16。這些名詞乍聽還可理解，一旦深入探究，就會發現背後需要紮實的數學功底。所以，很多介紹ZK的內容，要麼是光彩奪目的概念科普，要麼是晦澀難懂的協議分析，彷彿置身於一片高深莫測的領域。今天這篇文章，希望能帶給你一種不同的體驗。我們將從一個簡單的除法證明問題出發，從工程實踐的角度帶你走近ZK的世界線。

在我們討論後續問題之前，我們先用一個實踐向的直觀視角來解釋一下ZK，以便後續討論時有一個共同的基礎。在智能合約和區塊鏈中應用ZK技術解決的核心問題是如何在不暴露答案本身的情況下，證明自己知道這個正確的答案，例如一個多項式方程的解。越過原理，只想說目前有成熟方法能夠實現這個目標：首先，將一個複雜的問題通過多個僅涉及乘法和加法的簡單問題加以描述；然後，將這些簡單問題轉換為矩陣和代表正解的witness相乘的形式；接下來，將矩陣轉化為verification-key；同時，witness則進一步轉換為proof。

簡而言之：一個複雜問題被轉化為一組特定的key，而答案被分解為多個witness，最終演變為proof；proof能夠用verification-key以固定的算法驗證。一方面驗證成功說明生成proof的人確實知道問題的正確答案，另一方面通過proof卻無法反推出原解，保護了隱私。這一驗證過程可以用於提款的同時不暴露存款憑證；也可以用於證明一個transaction引發的合約代碼執行結果的真實性，進而用短proof代替多人執行transaction造成的資源消耗。

約束挑戰

由於ZK所有相關計算都在橢圓曲線上進行，只有加法和乘法是直接定義的。要證明一個複雜問題，必須將其拆解成包含這些基本運算的簡單子問題，即電路化。電路化的過程也是目前出問題最多的地方。

拆分出來的簡單的子問題被稱為“約束”，它們聯立后必須與原始複雜問題等效。如果某個約束缺失，可能導致構造出符合所有約束但不是正確答案的witness，從而偽造證明。這些偽造的證明仍然能夠通過verification-key的檢查，帶來一系列嚴重後果：如合約級別的雙重支付、或者zkVM級別的修改計算中間結果等。另一方面，若約束過於嚴格，超出了原問題的需求，則可能導致無法找到合適的witness，進而導致交易無法被證明，造成鏈級別的拒絕服務攻擊或合約應用的功能失效。第一種利用欠約束偽造證明看起來更有趣，它相當於直接控制了執行過程，類比於傳統安全漏洞利用時的控PC指針。

除法的案例分析

下面就來看一個簡單的除法問題在ZK的語境下該怎麼約束，又能惹出多少亂子。

設想如下場景，zkVM在運行時，執行了一個a除以b的運算，且我們要證明商是q，餘數是r。在這裏，a、b、q、r都是witness，我們需要確保它們滿足除法的約束。假設a和b已經由前序執行過程約束確定，我們僅關注q和r的約束。直覺上，既然a=b*q+r是除法的乘法表達形式，是不是一個約束多項式就夠用了呢？絕對不是！在實際的工程實現中，情況要複雜得多。例如，zkSync曾經的除法驗證過程涉及的代碼如下：

首先，a（src0_view）和b（src1_view）通過allocate_div_result_unchecked計算出q和r，這部分僅僅是算數運算，先驗地根據a和b求出作為witness的q和r，不涉及約束。

出於優化考慮，zkSync將乘法和除法放在同一個函數里進行約束，所以接下來是根據乘或除，通過帶有約束的選擇器取出要約束的變量，即r、q、b、a，並增加乘法約束MulDivRelation，也就是要求a=b*q+r。

MulDivRelation的乘法約束在指令循環即將結束前才由enforce_mul_relation函數施加。然而，由於zkSync選擇了Goldilock域（域階為0xffffffff00000001），這個域空間並不足以表示所有的uint64類型數據。因此，uint256需要分解成八個uint32來記錄。為了處理這部分的乘法，系統採用了逐輪計算的方式，每一輪通過fma_with_carry門對兩個uint32執行乘法約束。

乘法結束時，先用一次enforce_equal門約束計算結果沒有進位，再用一次保證乘加的累積結果和a相等。第二個enforce_equal的目的容易理解，也就是用於滿足我們之前反覆提及的a=b*q+r。

第一個沒有進位的約束確保了商q和餘數r的值不會超出預期的範圍，避免了計算結果出現溢出。除了進位檢查，另一個常用方法是約束比特長度（通過限制商和餘數比特數，確保計算的結果符合預期的範圍）。zkSync記得帶上了這個約束，但其實這是個很容易被忽略的細節，比如renegade項目計算fee相關用到的除法就漏掉過這個約束：

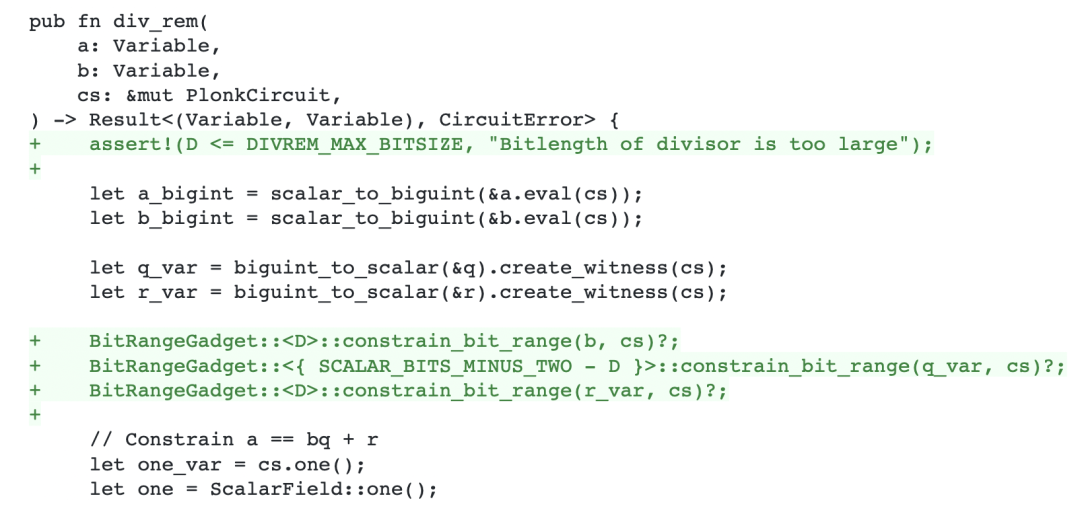
再比如Circom中的大整數求模庫函數Bigmod也曾出現過類似的漏洞。具體來說，Bigmod函數在實現過程中，只檢查了商q的比特長度，而忽略了對餘數r的長度檢測：

之所以要有這個約束，是因為有限域內的溢出會讓結果回滾仍落入域內，使得q和r不唯一。比如給定一個新的r=(a-r使攻擊者修改除法計算結果。對於日常使用的a和b，這樣修改r通常會導致一個非常大的q。

在zkSync的代碼中，乘法約束的設置只是第一步。接下來，它要比較r和b（除數），確保r<b。具體來說，allocate_subtraction_result_unchecked執行了這一比較操作，它做的只是計算出r-b，並將結果存入變量subtraction_result_unchecked和remainder_is_less_than_divisor。其中remainder_is_less_than_divisor記錄了長減法是否發生了借位。借位了則意味着r<b，這是我們期望看到的情況（由conditionally_enforce_true約束保證正確性）。之後b、r-b (subtraction_result_unchecked)、r、of(remainder_is_less_than_divisor)會被放入AddSubRelation。

在指令循環結束前，通過enforce_addition_relation函數施加UIntXAddGate加法門約束。確保(r-b)+b=r+of*2^256，其中of代表的是加法過程中產生的進位。這個約束的邏輯在於，r-b的結果應該為負數，域內表現為一個非常大的正數。為了讓這個結果能夠被正確表示，r-b與b相加時，必然會超過2^256導致進位，使得remainder_is_less_than_divisor的約束得以滿足：

這麼一套約束的目的是避免攻擊者通過構造另一組商q來繞過除法約束，進而偽造計算結果。比如我們設定新的q=r+b*k，很容易就找到了一組也符合乘法關係的witness篡改計算結果。這個約束在實際代碼中也很容易被忽略。例如，Polygon項目就曾經在代碼中誤加了過於寬鬆的r<a約束：

在zkSync的除法計算過程中，表面上看似乎所有必要的約束都已經施加，但代碼實現上仍然存在漏洞。這個漏洞和zkSync的代碼設計相關，之前提到，uint256類型的數據是通過八個uint32表示的，而每個uint32背後實際上是variable類型，它代表的是Goldilock域中的元素。因此，每個variable實際上最大可以表示0xffffffff00000000。

如果希望uint32中的variable僅表示32位整數，則必須為每個uint32額外施加比特長度約束，以確保其數值範圍受限。但在allocate_subtraction_result_unchecked函數中，並沒有對計算結果subtraction_result_unchecked中的每個uint32施加這種比特長度約束。這意味着，雖然subtraction_result_unchecked被定義為[uint32; 8]，但其中每個uint32實際上表示的最大值是0xffffffff00000000，而不是期望的32位限制。

因此，如果把subtraction_result_unchecked中最後一個uint32的第32比特篡改為1，則後面加法門的計算過程中必然會有進位，使得remainder_is_less_than_divisor約束天然滿足。之後令r=q-k就可以產生同樣合法的q和r的組合了。

總結

通過探討除法約束在工程實現中一些tricky的細節，我們初步感受了一下ZK世界的複雜與精妙。每個細節都可能隱藏着影響整個系統安全性的潛在風險，也正是這些細微之處構成了ZK證明技術的核心，推動了其在區塊鏈領域的廣泛應用。未來的篇章里，CertiK會繼續深入ZK的技術細節，敬請期待。

​